Vrijeme: 17:58
From Russia With log | From Russia With log #4
Kažemo da je niz brojeva 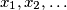 geometrijski ako postoje brojevi
geometrijski ako postoje brojevi  i
i  takvi da je
takvi da je 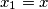 i za svaki sljedeći član niza vrijedi
i za svaki sljedeći član niza vrijedi 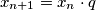 . Koliko ima parova prirodnih brojeva
. Koliko ima parova prirodnih brojeva 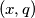 koji zadovoljavaju
koji zadovoljavaju 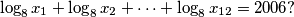
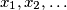 geometrijski ako postoje brojevi
geometrijski ako postoje brojevi  i
i  takvi da je
takvi da je 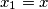 i za svaki sljedeći član niza vrijedi
i za svaki sljedeći član niza vrijedi 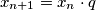 . Koliko ima parova prirodnih brojeva
. Koliko ima parova prirodnih brojeva 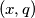 koji zadovoljavaju
koji zadovoljavaju 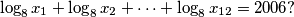
A sequence of numbers 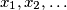 is called geometric if one can find numbers
is called geometric if one can find numbers  and
and  such that
such that 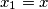 and every other term satisfies the condition
and every other term satisfies the condition 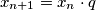 . How many ordered pairs
. How many ordered pairs 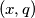 of positive integers are there that satisfy the equation
of positive integers are there that satisfy the equation 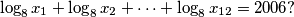
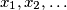 is called geometric if one can find numbers
is called geometric if one can find numbers  and
and  such that
such that 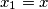 and every other term satisfies the condition
and every other term satisfies the condition 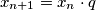 . How many ordered pairs
. How many ordered pairs 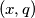 of positive integers are there that satisfy the equation
of positive integers are there that satisfy the equation