Nađi najveći realni broj
tako da ako su
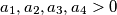
takvi da za sve
,
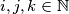
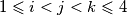
vrijedi
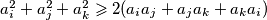
, onda nužno vrijedi i
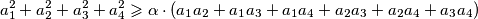
[lang=hr]
Nađi najveći realni broj $\alpha$ tako da ako su $a_1, a_2, a_3, a_4 >0$ takvi da za sve $i,j,k \in \mathbb{N}$, $1\leqslant i<j<k \leqslant 4$ vrijedi $a_{i}^2+a_{j}^2+a_{k}^2 \geqslant 2 (a_{i}a_{j}+a_{j}a_{k}+a_{k}a_{i})$, onda nužno vrijedi i
$$a_1^2+a_2^2+a_3^2+a_4^2\geqslant \alpha \cdot(a_1a_2+a_1a_3+a_1a_4+a_2a_3+a_2a_4+a_3a_4)$$
[/lang]
[lang=en]
Find the largest real number $\alpha$ such that: if $a_1, a_2, a_3, a_4 >0$ are such that for all $i,j,k \in \mathbb{N}$, $1\leqslant i<j<k \leqslant 4$ the expression $a_{i}^2+a_{j}^2+a_{k}^2 \geqslant 2 (a_{i}a_{j}+a_{j}a_{k}+a_{ k}a_{i})$ is valid, then necessarily the expression
$$a_1^2+a_2^2+a_3^2+a_4^2\geqslant \alpha \cdot(a_1a_2+a_1a_3+a_1a_4+a_2a_3+a_2a_4+a_3a_4)$$
is valid as well.
[/lang]
is valid, then necessarily the expression