Vrijeme: 17:59
Ma nije ovo TB... | No...this isn't number theory #4
Graf, sastavljen od 2022 vrhova imenovanim brojevima 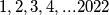 je zadan tako da su vrhovi
je zadan tako da su vrhovi  povezani ako i samo ako vrijedi
povezani ako i samo ako vrijedi 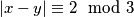 ili
ili  . Odredi kromatski broj grafa (Kromatski broj je minimalan broj boja potreban da se vrhovi grafa oboje tako da dva susjedna vrha nisu iste boje). NAPOMENA: nijedan vrh grafa nije povezan sam sa sobom.
. Odredi kromatski broj grafa (Kromatski broj je minimalan broj boja potreban da se vrhovi grafa oboje tako da dva susjedna vrha nisu iste boje). NAPOMENA: nijedan vrh grafa nije povezan sam sa sobom.
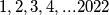 je zadan tako da su vrhovi
je zadan tako da su vrhovi  povezani ako i samo ako vrijedi
povezani ako i samo ako vrijedi 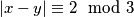 ili
ili  . Odredi kromatski broj grafa (Kromatski broj je minimalan broj boja potreban da se vrhovi grafa oboje tako da dva susjedna vrha nisu iste boje). NAPOMENA: nijedan vrh grafa nije povezan sam sa sobom.
. Odredi kromatski broj grafa (Kromatski broj je minimalan broj boja potreban da se vrhovi grafa oboje tako da dva susjedna vrha nisu iste boje). NAPOMENA: nijedan vrh grafa nije povezan sam sa sobom. Graph, constructed out of 2022 vertices named by the numbers 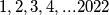 contains an edge
contains an edge 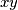 so that the statement (
so that the statement ( 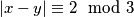 or
or  ) is true. Determine the chromatic number of the graph (Chromatic number is the minimal number of coulors necessary to paint the vertices of a graph so that two neighbouring vertices are not the same coulor). NOTE: a vertex of the graph is not connected to itself.
) is true. Determine the chromatic number of the graph (Chromatic number is the minimal number of coulors necessary to paint the vertices of a graph so that two neighbouring vertices are not the same coulor). NOTE: a vertex of the graph is not connected to itself.
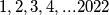 contains an edge
contains an edge 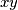 so that the statement (
so that the statement ( 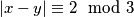 or
or  ) is true. Determine the chromatic number of the graph (Chromatic number is the minimal number of coulors necessary to paint the vertices of a graph so that two neighbouring vertices are not the same coulor). NOTE: a vertex of the graph is not connected to itself.
) is true. Determine the chromatic number of the graph (Chromatic number is the minimal number of coulors necessary to paint the vertices of a graph so that two neighbouring vertices are not the same coulor). NOTE: a vertex of the graph is not connected to itself. 