Neka su
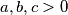
pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita:
![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png)
Odgovor zapišite kao niz od
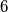
elemenata od kojih je svaki
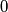
(nije nužno istinita tvrdnja) ili
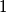
(nužno istinita tvrdnja). Primjerice
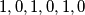
.
Let
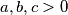
be positive real numbers. For each of the following claims determine whether it necessarily holds true:
![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png)
Write the answer as a sequence of
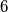
elements, each of which is either a
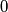
(the claim isn't necessarily true) or a
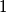
(the claim is necessarily true). E.g.
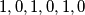
.
[lang=hr]
Neka su \(a,b,c > 0\) pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita:
\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}
Odgovor zapišite kao niz od \(6\) elemenata od kojih je svaki \(0\) (nije nužno istinita tvrdnja) ili \(1\) (nužno istinita tvrdnja). Primjerice \(1,0,1,0,1,0\).
[/lang]
[lang=en]
Let \(a,b,c > 0\) be positive real numbers. For each of the following claims determine whether it necessarily holds true:
\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}
Write the answer as a sequence of \(6\) elements, each of which is either a \(0\) (the claim isn't necessarily true) or a \(1\) (the claim is necessarily true). E.g. \(1,0,1,0,1,0\).
[/lang]
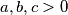 pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita:
pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita: ![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png) Odgovor zapišite kao niz od
Odgovor zapišite kao niz od 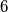 elemenata od kojih je svaki
elemenata od kojih je svaki 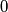 (nije nužno istinita tvrdnja) ili
(nije nužno istinita tvrdnja) ili 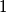 (nužno istinita tvrdnja). Primjerice
(nužno istinita tvrdnja). Primjerice 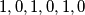 .
. 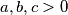 pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita:
pozitivni realni brojevi. Za svaku od sljedećih tvrdnji odredi je li ona nužno istinita: ![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png) Odgovor zapišite kao niz od
Odgovor zapišite kao niz od 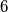 elemenata od kojih je svaki
elemenata od kojih je svaki 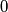 (nije nužno istinita tvrdnja) ili
(nije nužno istinita tvrdnja) ili 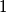 (nužno istinita tvrdnja). Primjerice
(nužno istinita tvrdnja). Primjerice 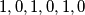 .
. 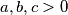 be positive real numbers. For each of the following claims determine whether it necessarily holds true:
be positive real numbers. For each of the following claims determine whether it necessarily holds true: ![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png) Write the answer as a sequence of
Write the answer as a sequence of 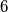 elements, each of which is either a
elements, each of which is either a 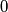 (the claim isn't necessarily true) or a
(the claim isn't necessarily true) or a 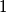 (the claim is necessarily true). E.g.
(the claim is necessarily true). E.g. 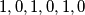 .
. 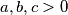 be positive real numbers. For each of the following claims determine whether it necessarily holds true:
be positive real numbers. For each of the following claims determine whether it necessarily holds true: ![\begin{enumerate}
\item \(\dfrac{a^2}{b} + \dfrac{b^2}{c} + \dfrac{c^2}{a} \geq a+b+c+ \dfrac{9(a-b)^2}{2(a+b+c)}\), % ne
\item \(a^3+b^3+c^3 \geq 3abc + 3|(a-b)(b-c)(a-c)|\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{c+a} > \dfrac{1}{3} \left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} + \dfrac{(\max\{a,b,c\} - \min \{a,b,c\})^2}{a+b+c} \right)\], % da
\item \(a+b+c \geq \sqrt[3]{abc} + 2\sqrt{\dfrac{a^2+b^2+c^2}{3}}\) % ne
\item \(\left( a+\dfrac{b}{2} + \dfrac{c}{3} \right) \left( a+2b+3c \right) \leq \dfrac{4}{3} (a+b+c)^2\), % da
\item Ako je \(a \neq b \neq c \neq a\), tada
\[\dfrac{a^2}{a+b} + \dfrac{b^2}{b+c} + \dfrac{c^2}{a+c} \geq \dfrac{1}{3}\left( \dfrac{a^3-b^3}{a^2-b^2} + \dfrac{b^3-c^3}{b^2-c^2} + \dfrac{c^3-a^3}{c^2-a^2} \right) + \dfrac{((a-b)(b-c)(c-a))^{\frac{4}{3}}}{(a+b)(b+c)(a+c)}\] % ne
\end{enumerate}](/media/m/e/b/c/ebc67cb722b15703ea042265f09b19aa.png) Write the answer as a sequence of
Write the answer as a sequence of 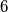 elements, each of which is either a
elements, each of which is either a 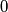 (the claim isn't necessarily true) or a
(the claim isn't necessarily true) or a 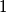 (the claim is necessarily true). E.g.
(the claim is necessarily true). E.g. 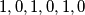 .
. 