Vrijeme: 18:00
Budi mi kutomjer? | Would you be my protractor? #3
Neka je  trokut s opisanom kružnicom
trokut s opisanom kružnicom  . Točka
. Točka  je središte luka
je središte luka  kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  , točka
, točka  je središte luka
je središte luka  kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  . Točka
. Točka  je na
je na  takva da je
takva da je  simetrala kuta
simetrala kuta  . Poznato nam je da vrijedi
. Poznato nam je da vrijedi 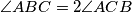 i
i 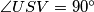 . Odredi
. Odredi 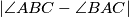 . (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
. (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
 trokut s opisanom kružnicom
trokut s opisanom kružnicom  . Točka
. Točka  je središte luka
je središte luka  kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  , točka
, točka  je središte luka
je središte luka  kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  . Točka
. Točka  je na
je na  takva da je
takva da je  simetrala kuta
simetrala kuta  . Poznato nam je da vrijedi
. Poznato nam je da vrijedi 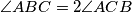 i
i 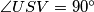 . Odredi
. Odredi 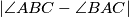 . (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
. (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45") Let  be a triangle with a circumscribed circle
be a triangle with a circumscribed circle  . Point
. Point  is the midpoint of circular arc
is the midpoint of circular arc  of circle
of circle  that doesn't contain point
that doesn't contain point  , point
, point  is the midpoint of circular arc
is the midpoint of circular arc  of circle
of circle  that doesn't cointain point
that doesn't cointain point  . Choose point
. Choose point  on
on  such that
such that  bisects angle
bisects angle  . Given that
. Given that 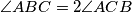 and
and 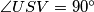 determine
determine 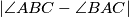 . (Write the solution in degrees but without measuring unit, e.g. "45".)
. (Write the solution in degrees but without measuring unit, e.g. "45".)
 be a triangle with a circumscribed circle
be a triangle with a circumscribed circle  . Point
. Point  is the midpoint of circular arc
is the midpoint of circular arc  of circle
of circle  that doesn't contain point
that doesn't contain point  , point
, point  is the midpoint of circular arc
is the midpoint of circular arc  of circle
of circle  that doesn't cointain point
that doesn't cointain point  . Choose point
. Choose point  on
on  such that
such that  bisects angle
bisects angle  . Given that
. Given that 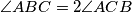 and
and 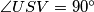 determine
determine 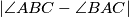 . (Write the solution in degrees but without measuring unit, e.g. "45".)
. (Write the solution in degrees but without measuring unit, e.g. "45".) 