Vrijeme: 17:59
Budi mi kutomjer? | Would you be my protractor? #5
Zadan je trokut  takav da vrijedi
takav da vrijedi 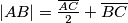 . Izvan trokuta konstruirana su dva polukruga kojima su promjeri
. Izvan trokuta konstruirana su dva polukruga kojima su promjeri  i
i  . Neka je
. Neka je  nožište iz
nožište iz  na zajedničku tangentu polukrugova. Odredi
na zajedničku tangentu polukrugova. Odredi 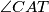 . (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
. (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
 takav da vrijedi
takav da vrijedi 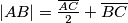 . Izvan trokuta konstruirana su dva polukruga kojima su promjeri
. Izvan trokuta konstruirana su dva polukruga kojima su promjeri  i
i  . Neka je
. Neka je  nožište iz
nožište iz  na zajedničku tangentu polukrugova. Odredi
na zajedničku tangentu polukrugova. Odredi 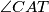 . (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45")
. (rješenje zapišite u stupnjevima bez mjerne jedinice npr. "45") Consider a triangle  in which
in which 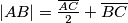 . Outside of that triangle we construct two semicircles with diameters
. Outside of that triangle we construct two semicircles with diameters  and
and  . Let
. Let  be the point at intersection of perpendicular from
be the point at intersection of perpendicular from  with the mutual tangent of semicircles. Determine
with the mutual tangent of semicircles. Determine 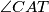 . (Write the solution in degrees but without measuring unit, e.g. "45".)
. (Write the solution in degrees but without measuring unit, e.g. "45".)
 in which
in which 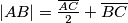 . Outside of that triangle we construct two semicircles with diameters
. Outside of that triangle we construct two semicircles with diameters  and
and  . Let
. Let  be the point at intersection of perpendicular from
be the point at intersection of perpendicular from  with the mutual tangent of semicircles. Determine
with the mutual tangent of semicircles. Determine 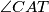 . (Write the solution in degrees but without measuring unit, e.g. "45".)
. (Write the solution in degrees but without measuring unit, e.g. "45".) 