Vrijeme: 18:02
Boris mi nije dao ime | Boris didn't name this one #1
Neka je  trokut u kome je
trokut u kome je 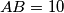 ,
, 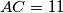 . Njemu upisana kružnica dodiruje
. Njemu upisana kružnica dodiruje 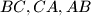 u
u 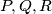 redom. Neka je
redom. Neka je  nožište visine iz
nožište visine iz  na
na 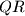 . Ako je
. Ako je 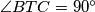 nađi
nađi  . Rješenje zaokruži na
. Rješenje zaokruži na  decimale.
decimale.
 trokut u kome je
trokut u kome je 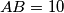 ,
, 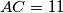 . Njemu upisana kružnica dodiruje
. Njemu upisana kružnica dodiruje 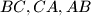 u
u 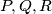 redom. Neka je
redom. Neka je  nožište visine iz
nožište visine iz  na
na 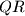 . Ako je
. Ako je 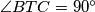 nađi
nađi  . Rješenje zaokruži na
. Rješenje zaokruži na  decimale.
decimale. Let  be a triangle in which
be a triangle in which 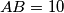 ,
, 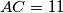 . The circle inscribed to it touches
. The circle inscribed to it touches 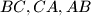 in
in 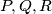 respectively. Let
respectively. Let  be the base of the height from
be the base of the height from  to
to 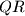 . If
. If 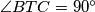 find
find  . Round the solution to
. Round the solution to  decimal places.
decimal places.
 be a triangle in which
be a triangle in which 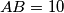 ,
, 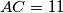 . The circle inscribed to it touches
. The circle inscribed to it touches 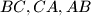 in
in 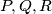 respectively. Let
respectively. Let  be the base of the height from
be the base of the height from  to
to 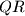 . If
. If 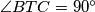 find
find  . Round the solution to
. Round the solution to  decimal places.
decimal places. 