Vrijeme: 17:58
Boris mi nije dao ime | Boris didn't name this one #2
U trokutu  s najvećom stranicom
s najvećom stranicom  vrijedi
vrijedi 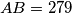 ,
,  . Neka je
. Neka je  polovište stranice
polovište stranice  ,
,  točka na stranici
točka na stranici  tako da je
tako da je  simetrala
simetrala  . Neka je
. Neka je  točka na
točka na  takva da je
takva da je 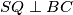 . Neka je
. Neka je 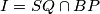 . Nađi
. Nađi 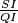 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale.
 s najvećom stranicom
s najvećom stranicom  vrijedi
vrijedi 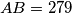 ,
,  . Neka je
. Neka je  polovište stranice
polovište stranice  ,
,  točka na stranici
točka na stranici  tako da je
tako da je  simetrala
simetrala  . Neka je
. Neka je  točka na
točka na  takva da je
takva da je 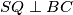 . Neka je
. Neka je 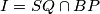 . Nađi
. Nađi 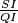 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale. In the triangle  with the largest side
with the largest side  ,
, 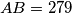 ,
,  is valid. Let
is valid. Let  be the midpoint of side
be the midpoint of side  ,
,  be a point on side
be a point on side  such that
such that  is the bisector of
is the bisector of  . Let
. Let  be a point on
be a point on  such that
such that 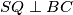 . Let
. Let 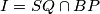 . Find
. Find 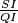 . Round the answer to 4 decimal places.
. Round the answer to 4 decimal places.
 with the largest side
with the largest side  ,
, 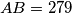 ,
,  is valid. Let
is valid. Let  be the midpoint of side
be the midpoint of side  ,
,  be a point on side
be a point on side  such that
such that  is the bisector of
is the bisector of  . Let
. Let  be a point on
be a point on  such that
such that 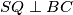 . Let
. Let 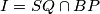 . Find
. Find 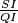 . Round the answer to 4 decimal places.
. Round the answer to 4 decimal places. 