Nešto me vuče na put, na put...Koda i Kenai su krenuli na put. Da ubije dosadu, Koda je sa sobom ponio  špagica, koje naravno sve skupa imaju
špagica, koje naravno sve skupa imaju  krajeva. Koda zatim
krajeva. Koda zatim  puta nasumično bira dva kraja, moguće i od iste špagice, te ih veže skupa (dva odabrana kraja su onda nadalje neupotrebljiva u igri).
puta nasumično bira dva kraja, moguće i od iste špagice, te ih veže skupa (dva odabrana kraja su onda nadalje neupotrebljiva u igri).
Koji je očekivani broj petlji kad Koda završi igru? U formalnom jeziku vjerojatnosti, ako je  broj petlji, odredi
broj petlji, odredi ![E[L]](/media/m/0/4/6/046071425fdd7d988c2f1e1b2b05824d.png) .
.
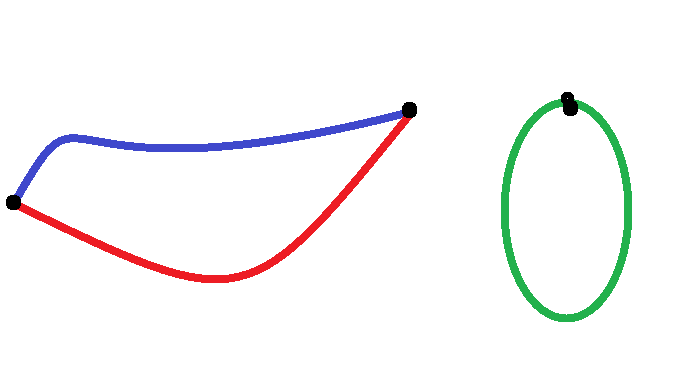
(Petlja je skup povezanih špagica. Na slici ispod možete vidjeti primjer dvije petlje od tri špagice.)
Tell everybody I'm on my way...
Koda and Kenai are going on an adventure. To cure his boredom, Koda brought  strings, which of course have
strings, which of course have  ends. Koda then randomly pairs two ends together, possibly from the same strings, and ties them together (the chosen two ends cannot be used again in the game). He repeats this process
ends. Koda then randomly pairs two ends together, possibly from the same strings, and ties them together (the chosen two ends cannot be used again in the game). He repeats this process  times until all string ends are used.
times until all string ends are used.
What is the expected number of loops when Koda finishes his game? In the formal language of probability, if  is the number of loops, calculate
is the number of loops, calculate ![E[L]](/media/m/0/4/6/046071425fdd7d988c2f1e1b2b05824d.png) .
.
(A loop is a set of connected strings. On the image below, you can see an example of two loops made out of three strings.

[lang=hr]
\textit{Nešto me vuče na put, na put...}
Koda i Kenai su krenuli na put. Da ubije dosadu, Koda je sa sobom ponio $100$ špagica, koje naravno sve skupa imaju $200$ krajeva. Koda zatim $100$ puta nasumično bira dva kraja, moguće i od iste špagice, te ih veže skupa (dva odabrana kraja su onda nadalje neupotrebljiva u igri).
Koji je očekivani broj petlji kad Koda završi igru? U formalnom jeziku vjerojatnosti, ako je $L$ broj petlji, odredi $E[L]$.
(\textit{Petlja je skup povezanih špagica. Na slici ispod možete vidjeti primjer dvije petlje od tri špagice.})
\includegraphics[scale=0.5]{petlja.png}
[/lang]
[lang=en]
\textit{Tell everybody I'm on my way...}
Koda and Kenai are going on an adventure. To cure his boredom, Koda brought $100$ strings, which of course have $200$ ends. Koda then randomly pairs two ends together, possibly from the same strings, and ties them together (the chosen two ends cannot be used again in the game). He repeats this process $100$ times until all string ends are used.
What is the expected number of loops when Koda finishes his game? In the formal language of probability, if $L$ is the number of loops, calculate $E[L]$.
(\textit{A loop is a set of connected strings. On the image below, you can see an example of two loops made out of three strings.}
\includegraphics[scale=0.5]{petlja.png}
[/lang]
 špagica, koje naravno sve skupa imaju
špagica, koje naravno sve skupa imaju  krajeva. Koda zatim
krajeva. Koda zatim  puta nasumično bira dva kraja, moguće i od iste špagice, te ih veže skupa (dva odabrana kraja su onda nadalje neupotrebljiva u igri).
puta nasumično bira dva kraja, moguće i od iste špagice, te ih veže skupa (dva odabrana kraja su onda nadalje neupotrebljiva u igri). broj petlji, odredi
broj petlji, odredi ![E[L]](/media/m/0/4/6/046071425fdd7d988c2f1e1b2b05824d.png) .
.
 strings, which of course have
strings, which of course have 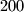 ends. Koda then randomly pairs two ends together, possibly from the same strings, and ties them together (the chosen two ends cannot be used again in the game). He repeats this process
ends. Koda then randomly pairs two ends together, possibly from the same strings, and ties them together (the chosen two ends cannot be used again in the game). He repeats this process  times until all string ends are used.
times until all string ends are used. is the number of loops, calculate
is the number of loops, calculate ![E[L]](/media/m/0/4/6/046071425fdd7d988c2f1e1b2b05824d.png) .
.
