Dan je realni broj
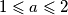
. Koja je najmanja moguća površina lika kojeg omeđuju grafovi funkcija
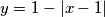
i
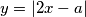
Given a real number
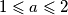
, what is the smallest possible area of the figure bounded by the graphs of the functions
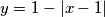
and
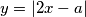
[lang=hr]
Dan je realni broj $1\leqslant a \leqslant 2$. Koja je najmanja moguća površina lika kojeg omeđuju grafovi funkcija
$$y = 1-|x-1|$$
i
$$y = |2x-a|$$
[/lang]
[lang=en]
Given a real number $1\leqslant a \leqslant 2$, what is the smallest possible area of the figure bounded by the graphs of the functions
$$y = 1-|x-1|$$
and
$$y = |2x-a|$$
[/lang]