Vrijeme: 17:58
Ekstremni uvjeti | Extreme conditions #3
Dani su realni brojevi 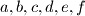 takvi da se polinom
takvi da se polinom 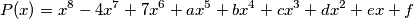 može prikazati kao umnožak
može prikazati kao umnožak  faktora oblika
faktora oblika 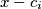 gdje je
gdje je 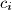 pozitivan za svaki od faktora.
pozitivan za svaki od faktora.
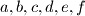 takvi da se polinom
takvi da se polinom 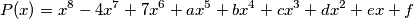 može prikazati kao umnožak
može prikazati kao umnožak  faktora oblika
faktora oblika 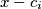 gdje je
gdje je 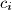 pozitivan za svaki od faktora.
pozitivan za svaki od faktora.Koja je najveća moguća vrijednost koeficijenta  ?
?
Real numbers 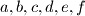 are given such that the polynomial
are given such that the polynomial 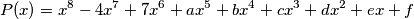 can be represented as a product of
can be represented as a product of  factors of the form
factors of the form 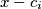 where
where 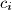 is positive for each of the factors.
is positive for each of the factors.
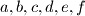 are given such that the polynomial
are given such that the polynomial 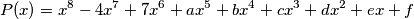 can be represented as a product of
can be represented as a product of  factors of the form
factors of the form 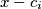 where
where 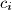 is positive for each of the factors.
is positive for each of the factors.What is the highest possible value of the coefficient  ?
?
