Vrijeme: 17:59
Crnogorski lanac | Montenegrian chain #4
Dan je prost broj  . Neka je
. Neka je 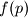 broj uređenih četvorki
broj uređenih četvorki 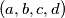 prirodnih brojeva koji nisu djeljivi s
prirodnih brojeva koji nisu djeljivi s  koje zadovoljavaju jednadžbe
koje zadovoljavaju jednadžbe 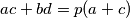 i
i 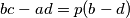 .
.
 . Neka je
. Neka je 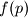 broj uređenih četvorki
broj uređenih četvorki 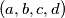 prirodnih brojeva koji nisu djeljivi s
prirodnih brojeva koji nisu djeljivi s  koje zadovoljavaju jednadžbe
koje zadovoljavaju jednadžbe 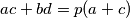 i
i 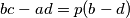 .
.Odredi zbroj 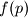 za sve proste
za sve proste 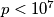 , tj.
, tj. 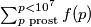 .
.
There is a prime number  . Let
. Let 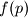 be the number of ordered fours
be the number of ordered fours 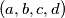 of natural numbers that are not divisible by
of natural numbers that are not divisible by  that satisfy the equations
that satisfy the equations 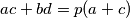 and
and 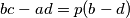 .
.
 . Let
. Let 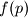 be the number of ordered fours
be the number of ordered fours 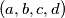 of natural numbers that are not divisible by
of natural numbers that are not divisible by  that satisfy the equations
that satisfy the equations 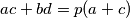 and
and 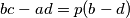 .
.Find the sum of 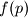 for all prime
for all prime 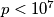 , that is
, that is 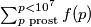 .
.
