Vrijeme: 08:28
Grafit | Graffiti #3
Matej ima stablo s 2028 čvorova označenim od 0 do 2027. Odlučio je od tog stabla napraviti niz od 2026 brojeva tako da odabere list s najmanjom oznakom, u niz doda oznaku njegovog jedinog susjeda te obriše odabrani list iz stabla. Ovaj postupak ponavlja dok ne popuni niz s 2026 brojeva. Sada Matej ima niz brojeva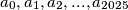 
takve da je 
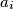najmanji nenegativan broj koji daje isti ostatak pri dijeljenju s 2027 kao i 
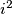. Zadivljen svojim nizom upitao se: "Kada bi iz početnog stabla obrisao čvor 4, dobio bi šumu koja se sastoji od nekoliko stabala. Koliki je umnožak veličine svakog takvog stabla?"
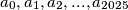takve da je 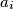najmanji nenegativan broj koji daje isti ostatak pri dijeljenju s 2027 kao i 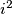. Zadivljen svojim nizom upitao se: "Kada bi iz početnog stabla obrisao čvor 4, dobio bi šumu koja se sastoji od nekoliko stabala. Koliki je umnožak veličine svakog takvog stabla?" Matej has a tree with 2028 vertices labeled from 0 to 2027. He decided to create an array of 2026 numbers from that tree such that he chooses a leaf with the lowest label, adds the label of his only neighbour at the end of the array and deletes the chosen leaf. He repeats this process until he fills the array with 2026 numbers. Now Matej has an array 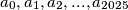such that 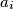is the smallest non-negative integer whose remainder modulo 2027 is the same as the remainder of 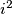. Fascinated with his array he asked himself: "If I were to delete vertex labeled 4 from the original tree I would obtain a forrest of some number of trees. What is the product of sizes of each such tree?"
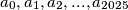such that 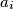is the smallest non-negative integer whose remainder modulo 2027 is the same as the remainder of 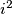. Fascinated with his array he asked himself: "If I were to delete vertex labeled 4 from the original tree I would obtain a forrest of some number of trees. What is the product of sizes of each such tree?"