Nakon što se riješio svih zaraženih vrećica, odlučio je na čajanku pozvati svoje prijatelje s Mostarskog Instituta za Tehnologiju.
S obzirom da za biznismena Harryja vrijeme drukčije teče, dan u njegovoj kući traje 2026 sati (označenih od 1 do 2026). Svaki prijatelj dolazi na početku nekog sata  i napušta čajanku na kraju nekog drugog sata
i napušta čajanku na kraju nekog drugog sata 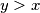 , pri čemu za svaki sat postoji točno jedna osoba koja ili dolazi ili odlazi (ali ne oboje). Naravno, svaka osoba mora doći i otići istoga dana (ne postoji osoba koja je samo došla ili samo otišla).
, pri čemu za svaki sat postoji točno jedna osoba koja ili dolazi ili odlazi (ali ne oboje). Naravno, svaka osoba mora doći i otići istoga dana (ne postoji osoba koja je samo došla ili samo otišla).
Harry mrzi kada neki od njegovih prijatelja prisustvuje i dolasku i odlasku nekog drugog prijatelja, te je zbog toga zamolio vas da mu kažete na koliko načina može pozvati svoje prijatelje da se ovo ne desi. Kako broj načina može biti vrlo velik, napišite ga kao ostatak pri dijeljenju s 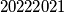 .
.
After getting rid of all the infected bags, he decided to invite his friends from the Mostar Institute of Technology to a tea party.
Given that time runs differently for businessman Harry, a day in his house lasts 2026 hours (marked from 1 to 2026). Each friend arrives at the beginning of some hour  and leaves the tea party at the end of some other hour
and leaves the tea party at the end of some other hour 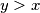 , where for each hour there is exactly one person who either arrives or leaves (but not both). Of course, each person must come and leave on the same day (there is no person who just came or just left).
, where for each hour there is exactly one person who either arrives or leaves (but not both). Of course, each person must come and leave on the same day (there is no person who just came or just left).
Harry hates it when one of his friends is present both at the arrival and the departure of another friend, so he asked you to tell him in how many ways he can invite his friends to prevent this from happening. Since the number of ways can be very large, type it as the remainder when dividing by 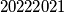 .
.
[lang=hr]
Nakon što se riješio svih zaraženih vrećica, odlučio je na čajanku pozvati svoje prijatelje s Mostarskog Instituta za Tehnologiju.
S obzirom da za biznismena Harryja vrijeme drukčije teče, dan u njegovoj kući traje 2026 sati (označenih od 1 do 2026). Svaki prijatelj dolazi na početku nekog sata $x$ i napušta čajanku na kraju nekog drugog sata $y>x$, pri čemu za svaki sat postoji točno jedna osoba koja ili dolazi ili odlazi (ali ne oboje). Naravno, svaka osoba mora doći i otići istoga dana (ne postoji osoba koja je samo došla ili samo otišla).
Harry mrzi kada neki od njegovih prijatelja prisustvuje i dolasku i odlasku nekog drugog prijatelja, te je zbog toga zamolio vas da mu kažete na koliko načina može pozvati svoje prijatelje da se ovo ne desi. Kako broj načina može biti vrlo velik, napišite ga kao ostatak pri dijeljenju s $20222021$.
[/lang]
[lang=en]
After getting rid of all the infected bags, he decided to invite his friends from the Mostar Institute of Technology to a tea party.
Given that time runs differently for businessman Harry, a day in his house lasts 2026 hours (marked from 1 to 2026). Each friend arrives at the beginning of some hour $x$ and leaves the tea party at the end of some other hour $y>x$, where for each hour there is exactly one person who either arrives or leaves (but not both). Of course, each person must come and leave on the same day (there is no person who just came or just left).
Harry hates it when one of his friends is present both at the arrival and the departure of another friend, so he asked you to tell him in how many ways he can invite his friends to prevent this from happening. Since the number of ways can be very large, type it as the remainder when dividing by $20222021$.
[/lang]
 i napušta čajanku na kraju nekog drugog sata
i napušta čajanku na kraju nekog drugog sata 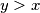 , pri čemu za svaki sat postoji točno jedna osoba koja ili dolazi ili odlazi (ali ne oboje). Naravno, svaka osoba mora doći i otići istoga dana (ne postoji osoba koja je samo došla ili samo otišla).
, pri čemu za svaki sat postoji točno jedna osoba koja ili dolazi ili odlazi (ali ne oboje). Naravno, svaka osoba mora doći i otići istoga dana (ne postoji osoba koja je samo došla ili samo otišla).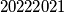 .
.  and leaves the tea party at the end of some other hour
and leaves the tea party at the end of some other hour 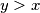 , where for each hour there is exactly one person who either arrives or leaves (but not both). Of course, each person must come and leave on the same day (there is no person who just came or just left).
, where for each hour there is exactly one person who either arrives or leaves (but not both). Of course, each person must come and leave on the same day (there is no person who just came or just left).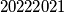 .
. 