Ako za
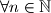
,

predstavlja broj realnih rješenja jednadžbe
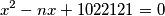
odredi zbroj 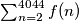 .
.
Let

be the number of real solutions to equation
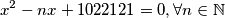
for
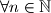
Determine
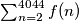
.
[lang=hr]
Ako za $\forall n \in \mathbb{N}$, $f(n)$ predstavlja broj realnih rješenja jednadžbe
$$x^2 - nx + 1022121 = 0$$
odredi zbroj $\sum_{n=2}^{4044} f(n)$.
[/lang]
[lang=en]
Let $f(n)$ be the number of real solutions to equation $$x^2 - nx + 1022121 = 0, \forall n \in \mathbb{N}$$ \\ for $\forall n \in \mathbb{N}$ \\
Determine $\sum_{n=2}^{4044} f(n)$.
[/lang]