Neka za
,
,
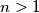
predstavlja broj kompleksnih rješenja jednadžbe
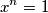
koja se nalaze u prvom kvadrantu ![[0, \pi/2]](/media/m/5/3/d/53dffe57f487796b2702c2ccdc44ec88.png)
.
Odredi zbroj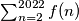 
.
Let for all
,
,
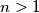
be the number or complex solutions to the equation
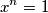
in the first quadrant
. Determine
.
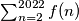
[lang=hr]
Neka za $n > 1$, $n \in \mathbb{N}$, $f(n)$ predstavlja broj kompleksnih rješenja jednadžbe
$$x^n = 1$$
koja se nalaze u prvom kvadrantu $[0, \pi/2]$.
Odredi zbroj $\sum_{n=2}^{2022} f(n)$.
[/lang]
[lang=en]
Let for all $n > 1$, $n \in \mathbb{N}$, $f(n)$ be the number or complex solutions to the equation $$x^n = 1$$ in the first quadrant $[0, \pi/2]$.
Determine $\sum_{n=2}^{2022} f(n)$.
[/lang]
