Podskup

skupa
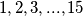
je takav da umnožak nikoja tri različita elementa

nije potpun kvadrat. Koliko najviše elemenata može imati

?
Subset

of a set
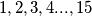
doesn't contain 3 different elements such that their product is a square. What is the largest number of elements that

can contain?
[lang=hr]
Podskup $A$ skupa $1, 2, 3, . . . ,15$ je takav da umnožak nikoja tri različita elementa $A$ nije potpun kvadrat. Koliko najviše elemenata može imati $A$?
[/lang]
[lang=en]
Subset $A$ of a set $1,2,3,4...,15$ doesn't contain 3 different elements such that their product is a square. What is the largest number of elements that $A$ can contain?
[/lang]