Vrijeme: 17:58
Lakše skupovne optimizacije | Easier set optimizations #5
Nađi najveći prirodan broj  koji zadovoljava sljedeću osobinu: Skup prirodnih brojeva možemo podijeliti na
koji zadovoljava sljedeću osobinu: Skup prirodnih brojeva možemo podijeliti na  podskupova
podskupova 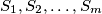 takve da za sve prirodne brojeve
takve da za sve prirodne brojeve 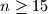 i sve
i sve 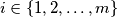 postoje dva različita elementa
postoje dva različita elementa 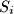 čija suma je
čija suma je  .
.
 koji zadovoljava sljedeću osobinu: Skup prirodnih brojeva možemo podijeliti na
koji zadovoljava sljedeću osobinu: Skup prirodnih brojeva možemo podijeliti na  podskupova
podskupova 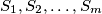 takve da za sve prirodne brojeve
takve da za sve prirodne brojeve 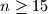 i sve
i sve 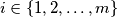 postoje dva različita elementa
postoje dva različita elementa 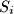 čija suma je
čija suma je  .
. Find the largest natural number  that satisfies the following property: The set of natural numbers can be divided into
that satisfies the following property: The set of natural numbers can be divided into  subsets
subsets 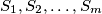 such that for all natural numbers
such that for all natural numbers 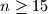 and all
and all 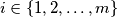 there are two different elements
there are two different elements 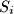 whose sum is
whose sum is  .
.
 that satisfies the following property: The set of natural numbers can be divided into
that satisfies the following property: The set of natural numbers can be divided into  subsets
subsets 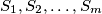 such that for all natural numbers
such that for all natural numbers 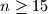 and all
and all 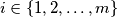 there are two different elements
there are two different elements 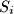 whose sum is
whose sum is  .
. 