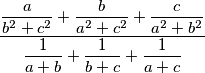Vrijeme: 17:59
Algebarske avanture prijatnog Lovre | Algebraic adventures of Lovre #2
Nakon par čaša dedinog domaćeg soka Lovro je odlučio krenuti na sljedeći zadatak koji glasi:
Neka su  nenegativni realni brojevi. Odredi miminum izraza:
nenegativni realni brojevi. Odredi miminum izraza:
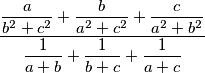
After a couple of glasses of his grandfather's homemade juice, Lovro decided to start the next task, which goes:
Let  be non-negative real numbers. Determine the minimum of the expression:
be non-negative real numbers. Determine the minimum of the expression: