Marinada '22

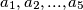[lang=hr] Lovro se već lagano počelo vrtjeti od količine soka od šljive koji je popio, no ustrajno je odlučio riješiti još zadataka. Zgrabio je još jedan s police, a na njemu je pisalo: Dan je niz od $5$ pozitivnih realnih brojeva $a_1,a_2, ... , a_5$ t.d. za svaki prirodan 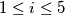$i$ ($1 \leq i \leq 5$) vrijedi 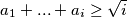$a_1+...+a_i \geq \sqrt{i}$, odredi najveći $M$ t.d. vrijedi $$a_1^2 + ... 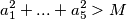+a_5^2 > M$$ [/lang] [lang=en] Lovro was already slightly dizzy from the amount of plum juice he drank, but he persistently decided to solve more tasks. He grabbed another one off the shelf, and it went: Given a sequence of $5$ positive real numbers $a_1,a_2, ... 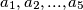, a_5$ so that for each natural number 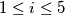$i$ ($1 \leq i \leq 5$) the expression 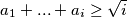$a_1+...+a_i \geq \sqrt{i}$ is true, determine the largest $M$ so that the following expression is valid: $$a_1^2 + ... +a_5^2 > M$$ [/lang]