Marinada '22

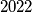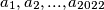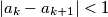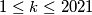[lang=hr] Lovro je shvatio da je popio cijelu bocu dedinog soka pa je krenuo po drugu, na putu je naišao na još jedan sladak zadatak koji galsi: Dano je $2022$ realnih brojeva $a_1,a_2, ... , a_{2022}$ većih od 1, za koje također vrijedi $|a_k - a_{k +1}| < 1$ za $1 \leq k \leq 2021$. 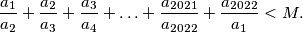Nađi najmanji $M$ tako da vrijedi $$ \dfrac{a_1}{a_2} + \dfrac{a_2}{a_3} + \dfrac{a_3}{a_4} + \ldots + \dfrac{a_{2021}}{a_{2022}} + \dfrac{a_{2022}}{a_1} < M .$$ Odgovor zaokružite na cijeli broj. [/lang] [lang=en] Lovro realized that he had drunk the whole bottle of grandfather's juice, so he went to get another one, on his way he came across another sweet task: 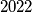$2022$ real numbers 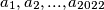$a_1,a_2, ... , a_{2022}$ all greater than 1 are given, for which the expression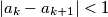$|a_k - a_{k +1}| < 1$ is valid for 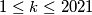$1 \leq k \leq 2021$. 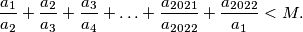Find the smallest $M$ so that the following is true: $$ \dfrac{a_1}{a_2} + \dfrac{a_2}{a_3} + \dfrac{a_3}{a_4} + \ldots + \dfrac{a_{2021}}{a_{2022}} + \dfrac{a_{2022} }{a_1} < M .$$ Round the answer to a whole number. [/lang]