Vrijeme: 17:58
Algebarske avanture prijatnog Lovre | Algebraic adventures of Lovre #5
Lovri je sada već teško pomaknuti se nakon 2 boce dedinog soka od šljiva, polako mu se sklapaju oči i kreće spavati. Budući da Lovro u sebi ima matematičarske gene on sanja sljedeći zadatak:
Neka je  prirodan broj. Neka je
prirodan broj. Neka je 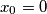 i neka je
i neka je 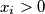 za svaki
za svaki 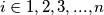 . Ako je
. Ako je 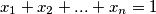 odredi najmanji
odredi najmanji  tako da vrijedi
tako da vrijedi 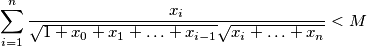 .
.
Odgovor zaokružite na 6 decimala.
It's already hard for Lovro to move after 2 bottles of grandfather's plum juice, his eyes slowly close and he goes to sleep. Since Lovro has mathematical genes in him, he dreams of the following task:
Let  be a natural number. Let
be a natural number. Let 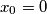 and let
and let 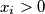 for every
for every 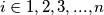 . If
. If 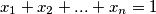 , determine the smallest
, determine the smallest  such that the following is true;
such that the following is true; 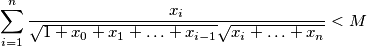 .
.
Round the answer to 6 decimal places.
