Vrijeme: 17:57
Ortocentričan sistem | Ortocentric system #5
U  ,
, 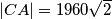 ,
, 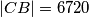 i
i  . Neka su
. Neka su  ,
,  ,
,  točke koje leže na
točke koje leže na  ,
,  i
i  takve da
takve da 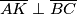 ,
, 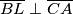 ,
, 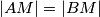 . Neka su
. Neka su  ,
,  ,
,  točke koje leže na
točke koje leže na 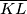 ,
, 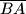 i
i 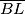 t.d. je
t.d. je 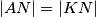 ,
, 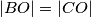 i
i  leži na
leži na 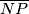 . Ako je
. Ako je  ortocentar od
ortocentar od 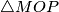 , izračunaj
, izračunaj  .
.
 ,
, 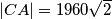 ,
, 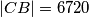 i
i  . Neka su
. Neka su  ,
,  ,
,  točke koje leže na
točke koje leže na  ,
,  i
i  takve da
takve da 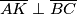 ,
, 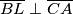 ,
, 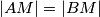 . Neka su
. Neka su  ,
,  ,
,  točke koje leže na
točke koje leže na 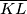 ,
, 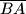 i
i 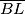 t.d. je
t.d. je 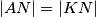 ,
, 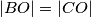 i
i  leži na
leži na 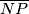 . Ako je
. Ako je  ortocentar od
ortocentar od 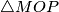 , izračunaj
, izračunaj  .
. In  ,
, 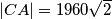 ,
, 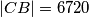 and
and  . Let
. Let  ,
,  ,
,  be points that lie on
be points that lie on  ,
,  and
and  such that
such that 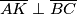 ,
, 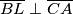 ,
, 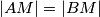 . Let
. Let  ,
,  ,
,  be points that lie on
be points that lie on 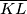 ,
, 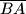 and
and 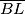 such that
such that 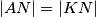 ,
, 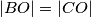 and
and  lies on
lies on 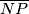 . If
. If  is the orthocenter of
is the orthocenter of 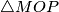 , determine
, determine  .
.
 ,
, 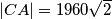 ,
, 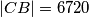 and
and  . Let
. Let  ,
,  ,
,  be points that lie on
be points that lie on  ,
,  and
and  such that
such that 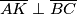 ,
, 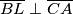 ,
, 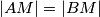 . Let
. Let  ,
,  ,
,  be points that lie on
be points that lie on 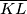 ,
, 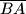 and
and 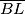 such that
such that 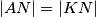 ,
, 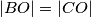 and
and  lies on
lies on 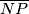 . If
. If  is the orthocenter of
is the orthocenter of 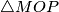 , determine
, determine  .
. 