S koliko najviše nula može završavati broj
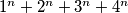
za

?
What is the maximal number of zeroes with which the number
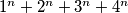
za

can end?
[lang=hr]
S koliko najviše nula može završavati broj $1^n+2^n+3^n+4^n$ za $n \in \mathbb{N}$?
[/lang]
[lang=en]
What is the maximal number of zeroes with which the number $1^n+2^n+3^n+4^n$ za $n \in \mathbb{N}$ can end?
[/lang]