Vrijeme: 17:59
Ortocentričan sistem | Ortocentric system #4
Neka je  šiljastokutan trokut s opisanom kružnicom
šiljastokutan trokut s opisanom kružnicom  i ortocentrom
i ortocentrom  . Pretpostavimo da pravac tangentan na opisanu kružnicu trokuta
. Pretpostavimo da pravac tangentan na opisanu kružnicu trokuta 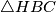 u
u  siječe
siječe  u točkama
u točkama  i
i  tako da vrijedi
tako da vrijedi 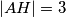 ,
, 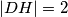 ,
, 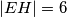 . Nađi površinu
. Nađi površinu  .
.
 šiljastokutan trokut s opisanom kružnicom
šiljastokutan trokut s opisanom kružnicom  i ortocentrom
i ortocentrom  . Pretpostavimo da pravac tangentan na opisanu kružnicu trokuta
. Pretpostavimo da pravac tangentan na opisanu kružnicu trokuta 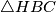 u
u  siječe
siječe  u točkama
u točkama  i
i  tako da vrijedi
tako da vrijedi 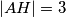 ,
, 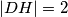 ,
, 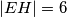 . Nađi površinu
. Nađi površinu  .
. Let  be an acute triangle with circumcircle
be an acute triangle with circumcircle  and orthocenter
and orthocenter  . Suppose the tangent to the circumcircle of
. Suppose the tangent to the circumcircle of 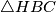 at
at  intersects
intersects  at points
at points  and
and  with
with 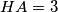 ,
, 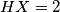 ,
, 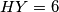 . Find the area of
. Find the area of  .
.
 be an acute triangle with circumcircle
be an acute triangle with circumcircle  and orthocenter
and orthocenter  . Suppose the tangent to the circumcircle of
. Suppose the tangent to the circumcircle of 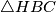 at
at  intersects
intersects  at points
at points  and
and  with
with 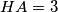 ,
, 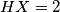 ,
, 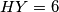 . Find the area of
. Find the area of  .
. 