Vrijeme: 17:58
Ortocentričan sistem | Ortocentric system #3
Neka je 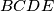 pravokutnik i neka je
pravokutnik i neka je  polovište
polovište 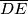 . Točka
. Točka  nalazi se na opisanoj kružnici pravokutnika. Označimo ortocentar trokuta
nalazi se na opisanoj kružnici pravokutnika. Označimo ortocentar trokuta 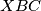 sa
sa  i neka je
i neka je  nožište okomice iz
nožište okomice iz  na pravac
na pravac 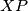 . Pretpostavimo da je
. Pretpostavimo da je 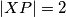 ,
, 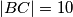 i da trokut
i da trokut 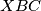 ima površinu
ima površinu 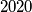 . Odredi
. Odredi 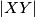 .
.
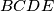 pravokutnik i neka je
pravokutnik i neka je  polovište
polovište 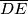 . Točka
. Točka  nalazi se na opisanoj kružnici pravokutnika. Označimo ortocentar trokuta
nalazi se na opisanoj kružnici pravokutnika. Označimo ortocentar trokuta 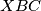 sa
sa  i neka je
i neka je  nožište okomice iz
nožište okomice iz  na pravac
na pravac 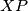 . Pretpostavimo da je
. Pretpostavimo da je 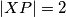 ,
, 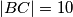 i da trokut
i da trokut 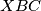 ima površinu
ima površinu 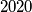 . Odredi
. Odredi 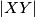 .
. Let 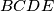 be a rectangle, let
be a rectangle, let  be the midpoint of
be the midpoint of 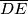 . Let
. Let  be a point on the circumcircle of the rectangle. Let triangle
be a point on the circumcircle of the rectangle. Let triangle 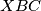 have orthocenter
have orthocenter  , and let
, and let  be the foot of the perpendicular from
be the foot of the perpendicular from  to line
to line 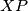 . Suppose that
. Suppose that 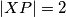 ,
, 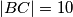 and area of
and area of 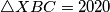 . Find
. Find 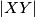 .
.
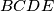 be a rectangle, let
be a rectangle, let  be the midpoint of
be the midpoint of 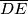 . Let
. Let  be a point on the circumcircle of the rectangle. Let triangle
be a point on the circumcircle of the rectangle. Let triangle 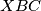 have orthocenter
have orthocenter  , and let
, and let  be the foot of the perpendicular from
be the foot of the perpendicular from  to line
to line 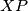 . Suppose that
. Suppose that 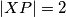 ,
, 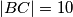 and area of
and area of 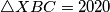 . Find
. Find 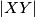 .
. 