Vrijeme: 17:59
Teže skupovne optimizacije | Harder set optimizations #2
Ako je  konačan neprazan skup prirodnih brojeva označimo sa
konačan neprazan skup prirodnih brojeva označimo sa 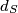 najveći prirodan broj koji dijeli sve elemente skupa
najveći prirodan broj koji dijeli sve elemente skupa  . Promatrajmo skup
. Promatrajmo skup  sa
sa 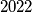 elementa koji zadovoljava da za svaka dva njegova neprazna podskupa
elementa koji zadovoljava da za svaka dva njegova neprazna podskupa 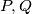 važi da
važi da 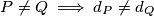 . Koliko najmanje prostih brojeva dijeli produkt svih elemenata skupa
. Koliko najmanje prostih brojeva dijeli produkt svih elemenata skupa  ?
?
 konačan neprazan skup prirodnih brojeva označimo sa
konačan neprazan skup prirodnih brojeva označimo sa 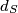 najveći prirodan broj koji dijeli sve elemente skupa
najveći prirodan broj koji dijeli sve elemente skupa  . Promatrajmo skup
. Promatrajmo skup  sa
sa 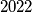 elementa koji zadovoljava da za svaka dva njegova neprazna podskupa
elementa koji zadovoljava da za svaka dva njegova neprazna podskupa 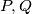 važi da
važi da 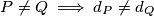 . Koliko najmanje prostih brojeva dijeli produkt svih elemenata skupa
. Koliko najmanje prostih brojeva dijeli produkt svih elemenata skupa  ?
? Let  be a finite nonempty set of natural numbers. Denote the largest natural number that divides all elements of
be a finite nonempty set of natural numbers. Denote the largest natural number that divides all elements of  with
with 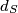 . Consider set
. Consider set  consisting of
consisting of 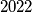 elements satisfying the condition that for every two of its nonempty sets
elements satisfying the condition that for every two of its nonempty sets  and
and 
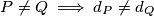 . What is the smallest possible number of prime numbers that divide the product of all elements from
. What is the smallest possible number of prime numbers that divide the product of all elements from  ?
?
 be a finite nonempty set of natural numbers. Denote the largest natural number that divides all elements of
be a finite nonempty set of natural numbers. Denote the largest natural number that divides all elements of  with
with 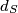 . Consider set
. Consider set  consisting of
consisting of 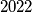 elements satisfying the condition that for every two of its nonempty sets
elements satisfying the condition that for every two of its nonempty sets  and
and 
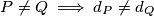 . What is the smallest possible number of prime numbers that divide the product of all elements from
. What is the smallest possible number of prime numbers that divide the product of all elements from  ?
? 