Vrijeme: 17:59
Teže skupovne optimizacije | Harder set optimizations #5
Skup  prirodnih brojeva je takav da postoji točno
prirodnih brojeva je takav da postoji točno  različitih prostih brojeva za koje postoji neki element skupa
različitih prostih brojeva za koje postoji neki element skupa  djeljiv s tim prostim brojem. Također nam je poznato da za svaki neprazan podskup skupa
djeljiv s tim prostim brojem. Također nam je poznato da za svaki neprazan podskup skupa  produkt njegovih elemenata nije potpuna
produkt njegovih elemenata nije potpuna 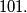 potencija. Koliko najviše elemenata može imati skup
potencija. Koliko najviše elemenata može imati skup  ?
?
 prirodnih brojeva je takav da postoji točno
prirodnih brojeva je takav da postoji točno  različitih prostih brojeva za koje postoji neki element skupa
različitih prostih brojeva za koje postoji neki element skupa  djeljiv s tim prostim brojem. Također nam je poznato da za svaki neprazan podskup skupa
djeljiv s tim prostim brojem. Također nam je poznato da za svaki neprazan podskup skupa  produkt njegovih elemenata nije potpuna
produkt njegovih elemenata nije potpuna 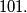 potencija. Koliko najviše elemenata može imati skup
potencija. Koliko najviše elemenata može imati skup  ?
? Set  consists of natural numbers so that there exist exactly
consists of natural numbers so that there exist exactly  different prime numbers for which there is some element from
different prime numbers for which there is some element from  divisible with that prime number. Given that for every nonempty subset
divisible with that prime number. Given that for every nonempty subset  product of its elements isn't a complete
product of its elements isn't a complete 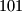 th power of any number. What is the greatest possible number of elements in
th power of any number. What is the greatest possible number of elements in  ?
?
 consists of natural numbers so that there exist exactly
consists of natural numbers so that there exist exactly  different prime numbers for which there is some element from
different prime numbers for which there is some element from  divisible with that prime number. Given that for every nonempty subset
divisible with that prime number. Given that for every nonempty subset  product of its elements isn't a complete
product of its elements isn't a complete 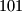 th power of any number. What is the greatest possible number of elements in
th power of any number. What is the greatest possible number of elements in  ?
? 