U trokutu

, točke

i

leže na
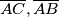
, redom. Označimo sa

presjek
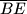
i

. Nađi najveću moguću površinu

ako je
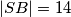
,
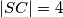
,
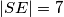
,
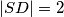
. Odgovor zaokruži na

decimale.
In

, points

and

lie on
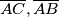
. Let

be an intersection between
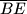
and

. Find the maximal surface of

if
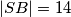
,
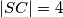
,
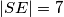
,
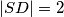
. Round the answer to 2 decimal points.
[lang=hr]
U trokutu $\triangle ABC$, točke $E$ i $D$ leže na $\overline{AC}, \overline{AB}$, redom. Označimo sa $S$ presjek $\overline{BE}$ i $\overline{CD}$. Nađi najveću moguću površinu $\triangle ABC$ ako je $|SB| = 14$, $|SC| = 4$, $|SE| = 7$, $|SD| = 2$. Odgovor zaokruži na $2$ decimale.
[/lang]
[lang=en]
In $\triangle ABC$, points $E$ and $D$ lie on $\overline{AC}, \overline{AB}$. Let $S$ be an intersection between $\overline{BE}$ and $\overline{CD}$. Find the maximal surface of $\triangle ABC$ if $|SB| = 14$, $|SC| = 4$, $|SE| = 7$, $|SD| = 2$. Round the answer to 2 decimal points.
[/lang]