Koliko ima brojeva
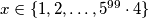
takvih da je
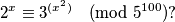
Find the number of integers
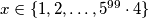
such that
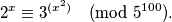
[lang=hr]
Koliko ima brojeva $x \in \{1, 2, \ldots, 5^{99} \cdot 4 \}$ takvih da je $$2^x \equiv 3^{(x^2)} \pmod{5^{100}}?$$
[/lang]
[lang=en]
Find the number of integers $x \in \{1, 2, \ldots, 5^{99} \cdot 4 \}$ such that $$2^x \equiv 3^{(x^2)} \pmod{5^{100}}.$$
[/lang]