Neka je
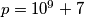
. Rekurzivno definiramo niz
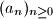
, tako da je
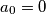
i
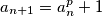
za
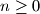
. Odredi najmanji prirodan broj

takav da
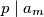
.
Let
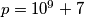
. Define a recursive sequence
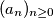
as follows:
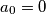
, and
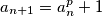
for
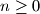
.Find the least positive integer

such that
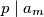
.
[lang=hr]
Neka je $p=10^9+7$. Rekurzivno definiramo niz $(a_n)_{n \geq 0}$, tako da je $a_0=0$ i $$a_{n+1}=a_n^p+1$$ za $n \geq 0$. Odredi najmanji prirodan broj $m$ takav da $p \mid a_m$.
[/lang]
[lang=en]
Let $p=10^9+7$. Define a recursive sequence $(a_n)_{ n \geq 0 }$ as follows: $a_0=0$, and $$a_{n+1}=a_n^p+1$$ for $n \geq 0$.Find the least positive integer $m$ such that $p \mid a_m$.
[/lang]