Vrijeme: 17:59
Niže | Niže #4
Za svaki neparan prost broj  , definiramo rekurzivan niz
, definiramo rekurzivan niz 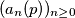 tako da je
tako da je 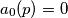 i
i 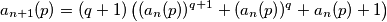 za
za 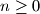 , gdje je
, gdje je 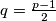 .
.
 , definiramo rekurzivan niz
, definiramo rekurzivan niz 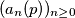 tako da je
tako da je 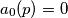 i
i 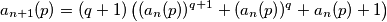 za
za 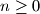 , gdje je
, gdje je 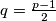 .
.Za prirodan broj 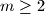 kažemo da je divan ako postoji prost
kažemo da je divan ako postoji prost  takav da
takav da 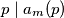 , te
, te 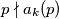 za svaki
za svaki 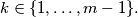 Drugim riječima,
Drugim riječima,  je najmanji pozitivan indeks takav da
je najmanji pozitivan indeks takav da 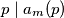 .
.
Koliko ima divnih brojeva manjih od 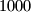 ?
?
For every odd prime  , define a recursive sequence
, define a recursive sequence 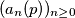 by
by 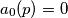 and
and 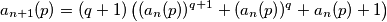 for
for 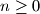 , where
, where 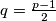 .
.
 , define a recursive sequence
, define a recursive sequence 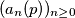 by
by 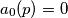 and
and 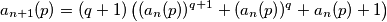 for
for 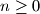 , where
, where 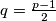 .
.We say a positive integer 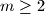 is lovely if there exists a prime number
is lovely if there exists a prime number  such that
such that 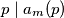 , and
, and 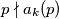 for every
for every 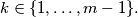 In other words,
In other words,  is the smallest positive index such that
is the smallest positive index such that 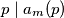 .
.
How many lovely numbers less than 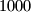 are there?
are there?
