Definiramo niz
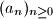
rekurzivno s
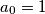
,
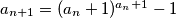
za
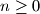
. Odredi najveći prirodan broj

takav da
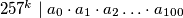
.
Define a sequence
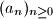
recursively by
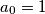
,
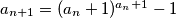
for
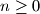
. Find the greatest positive integer

such that
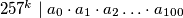
.
[lang=hr]
Definiramo niz $(a_n)_{n \geq 0}$ rekurzivno s $a_0=1$, $a_{n+1}=(a_n+1)^{a_n+1}-1$ za $n \geq 0$. Odredi najveći prirodan broj $k$ takav da $257^k \mid a_0\cdot a_1 \cdot a_2\ldots \cdot a_{100}$.
[/lang]
[lang=en]
Define a sequence $(a_n)_{n \geq 0}$ recursively by $a_0=1$, $a_{n+1}=(a_n+1)^{a_n+1}-1$ for $n \geq 0$. Find the greatest positive integer $k$ such that $257^k \mid a_0\cdot a_1 \cdot a_2\ldots \cdot a_{100}$.
[/lang]