Vrijeme: 18:02
Niže | Niže #3
Definiramo niz 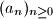 rekurzivno s
rekurzivno s 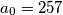 ,
, 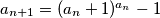 za
za 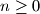 . Odredi najveći prirodan broj
. Odredi najveći prirodan broj  takav da
takav da 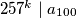 .
.
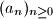 rekurzivno s
rekurzivno s 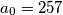 ,
, 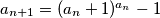 za
za 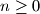 . Odredi najveći prirodan broj
. Odredi najveći prirodan broj  takav da
takav da 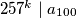 .
.S obzirom da je traženi broj velik, napišite samo njegove zadnje  znamenke, u formatu četveroznamenkastog broja.
znamenke, u formatu četveroznamenkastog broja.
Define a sequence 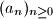 recursively by
recursively by 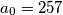 ,
, 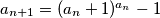 for
for 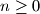 . Find the greatest positive integer
. Find the greatest positive integer  such that
such that 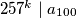 .
.
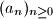 recursively by
recursively by 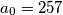 ,
, 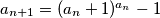 for
for 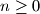 . Find the greatest positive integer
. Find the greatest positive integer  such that
such that 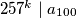 .
.Since this number is large, write only the last  digits, in the form of a
digits, in the form of a  -digit integer.
-digit integer.
