Idemo, druga runda!
1) Ako je neki broj prost i veći od 3, tada on daje ostatak 1 ili 5 pri dijeljenju sa 6.
2) Postoji potencija broja 3 čija je posljednja znamenka 2.
3) Postoji potencija broja 2 čija je posljednja znamenka 3.
4) Ako je broj a djeljiv brojem b, tada je umnožak 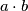 djeljiv s
djeljiv s 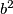 .
.
5) Ako je broj  djeljiv brojem
djeljiv brojem  , te broj
, te broj  djeljiv brojem
djeljiv brojem  , tada je zbroj
, tada je zbroj 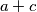 također djeljiv s
također djeljiv s  .
.
Let's go, round 2!
1) If a number is prime and greater than 3, then it gives a remainder of 1 or 5 when divided by 6.
2) There is a power of 3 whose last digit is 2.
3) There is a power of 2 whose last digit is 3.
4) If the number a is divisible by the number b, then the product 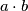 is divisible by
is divisible by 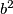 .
.
5) If the number  is divisible by the number
is divisible by the number  , and the number
, and the number  is divisible by the number
is divisible by the number  , then the sum
, then the sum 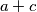 is also divisible by
is also divisible by  .
.
[lang=hr]
Idemo, druga runda!
1) Ako je neki broj prost i veći od 3, tada on daje ostatak 1 ili 5 pri dijeljenju sa 6.
2) Postoji potencija broja 3 čija je posljednja znamenka 2.
3) Postoji potencija broja 2 čija je posljednja znamenka 3.
4) Ako je broj a djeljiv brojem b, tada je umnožak $a \cdot b$ djeljiv s $b^2$.
5) Ako je broj $a$ djeljiv brojem $b$, te broj $c$ djeljiv brojem $b$, tada je zbroj $a+c$ također djeljiv s $b$.
[/lang]
[lang=en]
Let's go, round 2!
1) If a number is prime and greater than 3, then it gives a remainder of 1 or 5 when divided by 6.
2) There is a power of 3 whose last digit is 2.
3) There is a power of 2 whose last digit is 3.
4) If the number a is divisible by the number b, then the product $a \cdot b$ is divisible by $b^2$.
5) If the number $a$ is divisible by the number $b$, and the number $c$ is divisible by the number $b$, then the sum $a+c$ is also divisible by $b$.
[/lang]
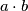 djeljiv s
djeljiv s 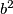 .
. djeljiv brojem
djeljiv brojem  , te broj
, te broj  djeljiv brojem
djeljiv brojem  , tada je zbroj
, tada je zbroj 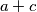 također djeljiv s
također djeljiv s  .
. 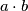 is divisible by
is divisible by 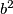 .
. is divisible by the number
is divisible by the number  , and the number
, and the number  is divisible by the number
is divisible by the number  , then the sum
, then the sum 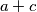 is also divisible by
is also divisible by  .
.