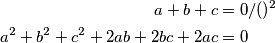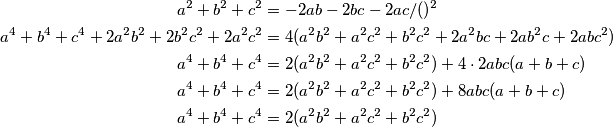Primjer 1. Dokažite da iz 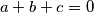 slijedi:
slijedi: 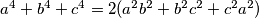 .
.
RJEŠENJE. Za početak potrebno je prvu jednakost kvadrirati; 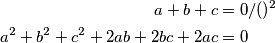
Zatim na desnoj strani ostavimo samo kvadrate kako bismo jednakost mogli opet kvadrirati; 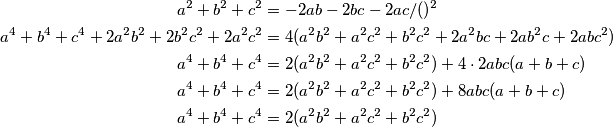
*Kako biste dobili 1 bod unesite 4 kao rješenje.
Example 1. Proof that given 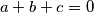 it holds:
it holds: 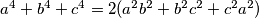 .
.
SOLUTION. For start you should square first equality; 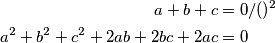
Then, on right side we just leave the squares so that we could square equality once again; 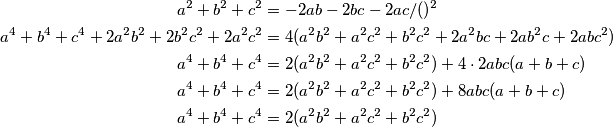
*To get 1 point, you should put 4 in the answer box.
[lang=en]
Primjer 1. Dokažite da iz $a + b + c = 0$ slijedi: $a^4 + b^4 + c^4 = 2(a^2b^2 + b^2c^2 + c^2a^2)$.\\ \\
RJEŠENJE.
Za početak potrebno je prvu jednakost kvadrirati;
\begin{align*}
a + b + c &= 0 /()^2\\
a^2 + b^2 + c^2 + 2ab + 2bc + 2ac &= 0
\end{align*}
Zatim na desnoj strani ostavimo samo kvadrate kako bismo jednakost mogli opet kvadrirati;
\begin{align*}
a^2 + b^2 + c^2 &= -2ab - 2bc - 2ac /()^2\\
a^4 + b^4 + c^4 + 2a^2b^2 + 2b^2c^2 + 2a^2c^2 &= 4(a^2b^2 + a^2c^2 + b^2c^2 + 2a^2bc + 2ab^2c + 2abc^2)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2+b^2c^2) + 4 \cdot 2abc(a + b + c)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2 + b^2c^2) + 8abc(a + b + c)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2 + b^2c^2) \\ \\
\end{align*}
*Kako biste dobili 1 bod unesite 4 kao rješenje.
[/lang]
[lang=hr]
Example 1. Proof that given $a + b + c = 0$ it holds: $a^4 + b^4 + c^4 = 2(a^2b^2 + b^2c^2 + c^2a^2)$.\\ \\
SOLUTION.
For start you should square first equality;
\begin{align*}
a + b + c &= 0 /()^2\\
a^2 + b^2 + c^2 + 2ab + 2bc + 2ac &= 0
\end{align*}
Then, on right side we just leave the squares so that we could square equality once again;
\begin{align*}
a^2 + b^2 + c^2 &= -2ab - 2bc - 2ac /()^2\\
a^4 + b^4 + c^4 + 2a^2b^2 + 2b^2c^2 + 2a^2c^2 &= 4(a^2b^2 + a^2c^2 + b^2c^2 + 2a^2bc + 2ab^2c + 2abc^2)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2+b^2c^2) + 4 \cdot 2abc(a + b + c)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2 + b^2c^2) + 8abc(a + b + c)\\
a^4 + b^4 + c^4 &= 2(a^2b^2 + a^2c^2 + b^2c^2) \\ \\
\end{align*}
*To get 1 point, you should put 4 in the answer box.
[/lang]
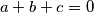 slijedi:
slijedi: 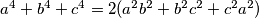 .
.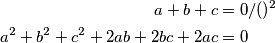
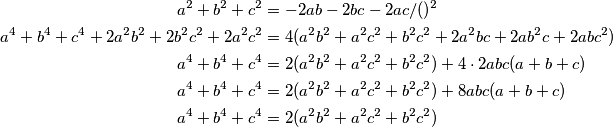
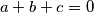 it holds:
it holds: 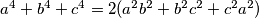 .
.