Za koliko prirodnih brojeva

takvih da
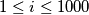
, postoji prirodan broj

takav da
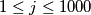
te da je

djelitelj od
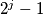
?
For how many natural numbers

such that
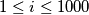
, there is a natural number

such that
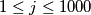
and that

is a divisor of
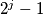
?
[lang = hr]
Za koliko prirodnih brojeva $i$ takvih da $1 \leq i \leq 1000$, postoji prirodan broj $j$ takav da $1 \leq j \leq 1000$ te da je $i$ djelitelj od $2^j-1$?
[/lang]
[lang = en]
For how many natural numbers $i$ such that $1 \leq i \leq 1000$, there is a natural number $j$ such that $1 \leq j \leq 1000$ and that $i$ is a divisor of $2^j-1$?
[/lang]