Odredi prirodne brojeve

i

,

,

,

takve da vrijedi
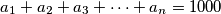
i da je umnožak
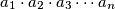
maksimalan.
Kao rješenje upiši 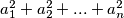 .
.
Determine the natural numbers

and

,

,

,

such that
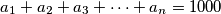
and that the product
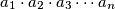
is maximal.
As a solution, write 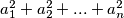 .
.
[lang = hr]
Odredi prirodne brojeve $n$ i $a_1$, $a_2$, $\dots$, $a_n$ takve da vrijedi
\[ a_1 + a_2 + a_3 + \dotsb + a_n = 1000 \]
i da je umnožak $a_1 \cdot a_2 \cdot a_3 \dotsb a_n$ maksimalan.
Kao rješenje upiši $a_1^2+a_2^2+...+a_n^2$.
[/lang]
[lang = en]
Determine the natural numbers $n$ and $a_1$, $a_2$, $\dots$, $a_n$ such that
\[ a_1 + a_2 + a_3 + \dotsb + a_n = 1000 \]
and that the product $a_1 \cdot a_2 \cdot a_3 \dotsb a_n$ is maximal.
As a solution, write $a_1^2+a_2^2+...+a_n^2$.
[/lang]