Vrijeme: 17:57
Sve samo ne komba | Everything but C #5
U 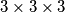 kocki nasumično je odabrano
kocki nasumično je odabrano  točaka i
točaka i  kocaka
kocaka 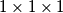 (svaka točka malih kocka sadržana je u velikoj kocki). Koliki je očekivan broj odabranih
(svaka točka malih kocka sadržana je u velikoj kocki). Koliki je očekivan broj odabranih 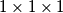 kocaka koje sadrže barem jednu označenom točku?
kocaka koje sadrže barem jednu označenom točku?
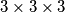 kocki nasumično je odabrano
kocki nasumično je odabrano  točaka i
točaka i  kocaka
kocaka 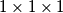 (svaka točka malih kocka sadržana je u velikoj kocki). Koliki je očekivan broj odabranih
(svaka točka malih kocka sadržana je u velikoj kocki). Koliki je očekivan broj odabranih 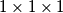 kocaka koje sadrže barem jednu označenom točku?
kocaka koje sadrže barem jednu označenom točku? In a 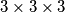 cube we randomly pick
cube we randomly pick  points and
points and  cubes
cubes 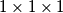 (every point of the little cubes is contained within the big cube). What is the expected number of chosen
(every point of the little cubes is contained within the big cube). What is the expected number of chosen 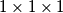 cubes which contain at least one chosen point
cubes which contain at least one chosen point
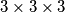 cube we randomly pick
cube we randomly pick  points and
points and  cubes
cubes 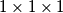 (every point of the little cubes is contained within the big cube). What is the expected number of chosen
(every point of the little cubes is contained within the big cube). What is the expected number of chosen 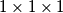 cubes which contain at least one chosen point
cubes which contain at least one chosen point 