Dane su točke
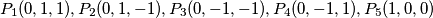
. Unutar piramide određene tim točkama nasumično odaberemo
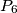
. Kolika je vjerojatnost da
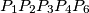
ima manji volumen od
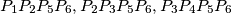
i
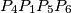
?
Given points
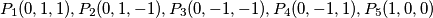
. Inside the pyramid determined by these points, we randomly select
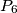
. What is the probability that
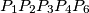
has a smaller volume than
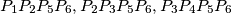
, and
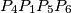
?
[lang = hr]
Dane su točke $P_1(0,1,1), P_2(0,1,-1), P_3(0,-1,-1), P_4(0,-1,1), P_5(1,0,0)$. Unutar piramide određene tim točkama nasumično odaberemo $P_6$. Kolika je vjerojatnost da $P_1P_2P_3P_4P_6$ ima manji volumen od $P_1P_2P_5P_6, P_2P_3P_5P_6, P_3P_4P_5P_6$ i $ P_4P_1P_5P_6$?
[/lang]
[lang = en]
Given points $P_1(0,1,1), P_2(0,1,-1), P_3(0,-1,-1), P_4(0,-1,1), P_5(1,0, 0)$. Inside the pyramid determined by these points, we randomly select $P_6$. What is the probability that $P_1P_2P_3P_4P_6$ has a smaller volume than $P_1P_2P_5P_6, P_2P_3P_5P_6, P_3P_4P_5P_6$, and $ P_4P_1P_5P_6$?
[/lang]