Vrijeme: 18:01
Zadnji teorem | Last theorem #3
Dano je 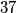 intervala
intervala ![[a_i,b_i]](/media/m/e/d/9/ed9b50c2caf1824e1482432c071513bd.png) (
( 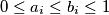 )gdje je
)gdje je  element skupa
element skupa 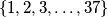 . Neovisno o odabiru
. Neovisno o odabiru  -ova i
-ova i  -ova možemo garantirati da postoji
-ova možemo garantirati da postoji  intervala s zajedničkim elementom ili
intervala s zajedničkim elementom ili  međusobno disjunktnih intervala. Koliko je
međusobno disjunktnih intervala. Koliko je  ?
?
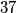 intervala
intervala ![[a_i,b_i]](/media/m/e/d/9/ed9b50c2caf1824e1482432c071513bd.png) (
( 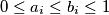 )gdje je
)gdje je  element skupa
element skupa 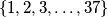 . Neovisno o odabiru
. Neovisno o odabiru  -ova i
-ova i  -ova možemo garantirati da postoji
-ova možemo garantirati da postoji  intervala s zajedničkim elementom ili
intervala s zajedničkim elementom ili  međusobno disjunktnih intervala. Koliko je
međusobno disjunktnih intervala. Koliko je  ?
? Given 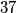 intervals
intervals ![[a_i,b_i]](/media/m/e/d/9/ed9b50c2caf1824e1482432c071513bd.png) (
( 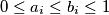 ) where
) where  is an element of the set
is an element of the set 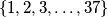 . Regardless of the choice of
. Regardless of the choice of  and
and  , we can guarantee that there are
, we can guarantee that there are  intervals with a common element or
intervals with a common element or  mutually disjoint intervals. How much is
mutually disjoint intervals. How much is  ?
?
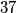 intervals
intervals ![[a_i,b_i]](/media/m/e/d/9/ed9b50c2caf1824e1482432c071513bd.png) (
( 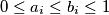 ) where
) where  is an element of the set
is an element of the set 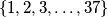 . Regardless of the choice of
. Regardless of the choice of  and
and  , we can guarantee that there are
, we can guarantee that there are  intervals with a common element or
intervals with a common element or  mutually disjoint intervals. How much is
mutually disjoint intervals. How much is  ?
? 