Vrijeme: 17:58
Beskorisna geogebra | Useless geogebra #2
Dan je jednakokračan  s osnovicom
s osnovicom  duljine
duljine  i krakovima duljine
i krakovima duljine 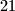 . Točke
. Točke 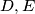 su redom na stranicama
su redom na stranicama 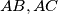 takve da je dužina
takve da je dužina  paralelna osnovici. Točka
paralelna osnovici. Točka  se nalazi unutar
se nalazi unutar  tako da je četverokut
tako da je četverokut 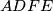 tetivan i vrijedi
tetivan i vrijedi 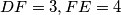 . Omjer površina četverokuta
. Omjer površina četverokuta 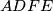 i
i  se može izraziti kao razlomak
se može izraziti kao razlomak 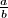 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Koliko je
relativno prosti prirodni brojevi. Koliko je  ?
?
 s osnovicom
s osnovicom  duljine
duljine  i krakovima duljine
i krakovima duljine 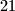 . Točke
. Točke 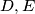 su redom na stranicama
su redom na stranicama 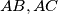 takve da je dužina
takve da je dužina  paralelna osnovici. Točka
paralelna osnovici. Točka  se nalazi unutar
se nalazi unutar  tako da je četverokut
tako da je četverokut 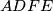 tetivan i vrijedi
tetivan i vrijedi 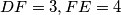 . Omjer površina četverokuta
. Omjer površina četverokuta 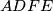 i
i  se može izraziti kao razlomak
se može izraziti kao razlomak 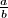 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Koliko je
relativno prosti prirodni brojevi. Koliko je  ?
? An isosceles  with a base
with a base  of length
of length  and legs of length
and legs of length 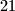 is given. The points
is given. The points 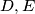 are respectively on the sides
are respectively on the sides 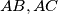 such that the
such that the  is parallel to the base. Point
is parallel to the base. Point  is inside
is inside  so that quadrilateral
so that quadrilateral 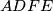 is cyclic and
is cyclic and 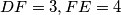 holds. The ratio of the areas of quadrilateral
holds. The ratio of the areas of quadrilateral 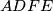 and
and  can be expressed as a fraction
can be expressed as a fraction 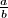 , where
, where  and
and  are relatively prime positive integers. What is the value of
are relatively prime positive integers. What is the value of  ?
?
 with a base
with a base  of length
of length  and legs of length
and legs of length 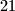 is given. The points
is given. The points 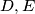 are respectively on the sides
are respectively on the sides 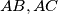 such that the
such that the  is parallel to the base. Point
is parallel to the base. Point  is inside
is inside  so that quadrilateral
so that quadrilateral 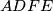 is cyclic and
is cyclic and 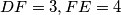 holds. The ratio of the areas of quadrilateral
holds. The ratio of the areas of quadrilateral 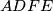 and
and  can be expressed as a fraction
can be expressed as a fraction 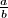 , where
, where  and
and  are relatively prime positive integers. What is the value of
are relatively prime positive integers. What is the value of  ?
? 