Neka su

prirodni brojevi takvi da je
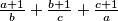
cijeli broj. Odredi najveći
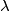
takav da je
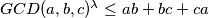
za sve takve trojke

.
Let

be positive integers such that
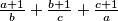
is an integer. Find the greatest
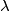
such that
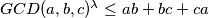
for all said triples

.
[lang=hr]
Neka su $a,b,c$ prirodni brojevi takvi da je $\frac{a+1}{b}+\frac{b+1}{c}+\frac{c+1}{a}$ cijeli broj. Odredi najveći $\lambda$ takav da je $GCD(a,b,c)^{\lambda} \leq ab+bc+ca$ za sve takve trojke $a,b,c$.
[/lang]
[lang=en]
Let $a,b,c$ be positive integers such that $\frac{a+1}{b}+\frac{b+1}{c}+\frac{c+1}{a}$ is an integer. Find the greatest $\lambda$ such that $GCD(a,b,c)^{\lambda} \leq ab+bc+ca$ for all said triples $a,b,c$.
[/lang]