Koji je nagib pravca koji prolazi kroz
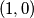
i da je pri tome dužina tetive koju određuje u kružnici
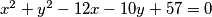
maksimalna moguća?
What is the slope of the line that passes through
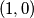
such that the length of the chord that it determines in the circle
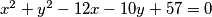
is the maximum possible?
[lang=hr]
Koji je nagib pravca koji prolazi kroz $(1,0)$ i da je pri tome dužina tetive koju određuje u kružnici $x^2+y^2-12x-10y+57=0$ maksimalna moguća?
[/lang]
[lang=en]
What is the slope of the line that passes through $(1,0)$ such that the length of the chord that it determines in the circle $x^2+y^2-12x-10y+57=0$ is the maximum possible?
[/lang]