Dane su točke
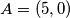
i
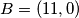
. Na kružnici
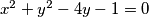
odabrana je točka

tako da je
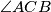
maksimalan. Koja je

-koordinata od

?
Points
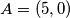
and
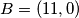
are given. On the circle
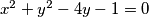
, the point

is chosen so that
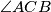
is maximal. What is the

-coordinate of

?
[lang=hr]
Dane su točke $A=(5,0)$ i $B=(11,0)$. Na kružnici $x^2 + y^2 - 4y -1=0$ odabrana je točka $C$ tako da je $\angle ACB$ maksimalan.
Koja je $x$-koordinata od $C$?
[/lang]
[lang=en]
Points $A=(5,0)$ and $B=(11,0)$ are given. On the circle $x^2 + y^2 - 4y -1=0$, the point $C$ is chosen so that $\angle ACB$ is maximal.
What is the $x$-coordinate of $C$?
[/lang]