Vrijeme: 17:58
Zadnji teorem | Last theorem #4
Zadan je potpun graf od 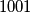 čvora. Bridovi su mu obojani u
čvora. Bridovi su mu obojani u  boja. Za svaku boju vrijedi: kada bismo gledali samo bridove odabrane boje, graf ne bi bio povezan. Za svaki par boja vrijedi: kada bismo gledali samo bridove koji su obojani u jednu od odabranih boja boje, graf bi bio povezan.
boja. Za svaku boju vrijedi: kada bismo gledali samo bridove odabrane boje, graf ne bi bio povezan. Za svaki par boja vrijedi: kada bismo gledali samo bridove koji su obojani u jednu od odabranih boja boje, graf bi bio povezan.
Kolika je najmanja vrijednost koju može poprimiti?
može poprimiti?
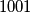 čvora. Bridovi su mu obojani u
čvora. Bridovi su mu obojani u  boja. Za svaku boju vrijedi: kada bismo gledali samo bridove odabrane boje, graf ne bi bio povezan. Za svaki par boja vrijedi: kada bismo gledali samo bridove koji su obojani u jednu od odabranih boja boje, graf bi bio povezan.
boja. Za svaku boju vrijedi: kada bismo gledali samo bridove odabrane boje, graf ne bi bio povezan. Za svaki par boja vrijedi: kada bismo gledali samo bridove koji su obojani u jednu od odabranih boja boje, graf bi bio povezan. Kolika je najmanja vrijednost koju
 može poprimiti?
može poprimiti? A complete graph of 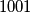 nodes is given. Its edges are painted in
nodes is given. Its edges are painted in  colors. It is true for every color: if we looked only at the edges of the selected color, the graph would not be connected. For every pair of colors it is true: if we were to look only at the edges that are colored in one of the selected colors, the graph would be connected.
colors. It is true for every color: if we looked only at the edges of the selected color, the graph would not be connected. For every pair of colors it is true: if we were to look only at the edges that are colored in one of the selected colors, the graph would be connected.
What is the smallest value that can take?
can take?
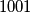 nodes is given. Its edges are painted in
nodes is given. Its edges are painted in  colors. It is true for every color: if we looked only at the edges of the selected color, the graph would not be connected. For every pair of colors it is true: if we were to look only at the edges that are colored in one of the selected colors, the graph would be connected.
colors. It is true for every color: if we looked only at the edges of the selected color, the graph would not be connected. For every pair of colors it is true: if we were to look only at the edges that are colored in one of the selected colors, the graph would be connected. What is the smallest value that
 can take?
can take? 