Odredite vrijednost sume
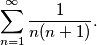
Formalno vrijedi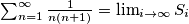 
, gdje je 
.
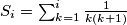HINT
Determine the value of
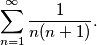
Formally, it holds that 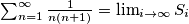, where .
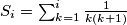HINT
[lang=hr]
Odredite vrijednost sume
$$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}.$$\\
Formalno vrijedi $\sum_{n=1}^{\infty}\frac{1}{n(n+1)} = \lim_{i\rightarrow \infty} S_i$, gdje je $S_i= \sum_{k=1}^{i}\frac{1}{k(k+1)} $.
\\
\href{https://www.youtube.com/watch?v=sIkfphkYUd4}{HINT}
[/lang]
[lang=en]
Determine the value of
$$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}.$$\\
Formally, it holds that $\sum_{n=1}^{\infty}\frac{1}{n(n+1)} = \lim_{i\rightarrow \infty} S_i$, where $S_i= \sum_{k=1}^{i}\frac{1}{k(k+1)} $.
\\
\href{https://www.youtube.com/watch?v=sIkfphkYUd4}{HINT}
[/lang]
