Vrijeme: 17:58
N 'n chill #3
Odredite sve 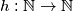 takve da
takve da 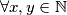 vrijedi
vrijedi
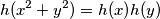
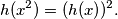
Rješenje zapišite tako da napišete prvih članova niza
članova niza  razdvojene zarezom gdje je:
razdvojene zarezom gdje je: 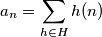
 je skup funkcija
je skup funkcija  koje zadovoljavaju uvjete zadatka.
koje zadovoljavaju uvjete zadatka.
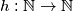 takve da
takve da 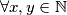 vrijedi
vrijedi 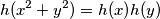
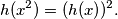
Rješenje zapišite tako da napišete prvih
 članova niza
članova niza  razdvojene zarezom gdje je:
razdvojene zarezom gdje je: 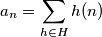
 je skup funkcija
je skup funkcija  koje zadovoljavaju uvjete zadatka.
koje zadovoljavaju uvjete zadatka. Determine all functions 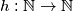 such that
such that 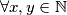
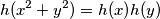
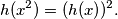
Give your solution by writing the first terms
terms  separated by a comma where:
separated by a comma where: 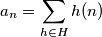
 is the set of functions
is the set of functions  which satisfy the problem statement.
which satisfy the problem statement.
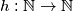 such that
such that 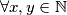
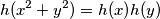
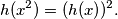
Give your solution by writing the first
 terms
terms  separated by a comma where:
separated by a comma where: 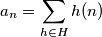
 is the set of functions
is the set of functions  which satisfy the problem statement.
which satisfy the problem statement. 