Pronađite najmanji
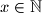
takav da je
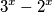
višekratnik broja
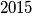
.
Find the smallest
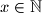
such that
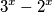
is a multiple of
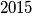
.
[lang = hr]
Pronađite najmanji $x \in \mathbb{N}$ takav da je
$$3^x-2^x$$
višekratnik broja $2015$.
[/lang]
[lang = en]
Find the smallest $x \in \mathbb{N}$ such that
$$3^x-2^x$$
is a multiple of $2015$.
[/lang]