Neka za beskonačan niz različitih realnih brojeva vrijedi 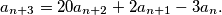
Ovisno o vrijednostima prva tri člana, izraz 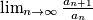 može poprimiti tri vrijednosti. Koji je zbroj tih vrijednosti?
može poprimiti tri vrijednosti. Koji je zbroj tih vrijednosti?
For an infinite sequence of different real numbers it holds that 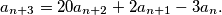
Depending on the values of the first three terms, the expression 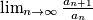 can take on three values. What is the sum of these values?
can take on three values. What is the sum of these values?
[lang=hr]
Neka za beskonačan niz različitih realnih brojeva vrijedi
$$a_{n+3}=20a_{n+2}+2a_{n+1}-3a_n.$$\\
Ovisno o vrijednostima prva tri člana, izraz $\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n}$ može poprimiti tri vrijednosti. Koji je zbroj tih vrijednosti?
[/lang]
[lang=en]
For an infinite sequence of different real numbers it holds that
$$a_{n+3}=20a_{n+2}+2a_{n+1}-3a_n.$$\\
Depending on the values of the first three terms, the expression $\lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n}$ can take on three values. What is the sum of these values?
[/lang]
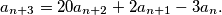
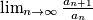 može poprimiti tri vrijednosti. Koji je zbroj tih vrijednosti?
može poprimiti tri vrijednosti. Koji je zbroj tih vrijednosti?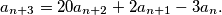
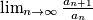 can take on three values. What is the sum of these values?
can take on three values. What is the sum of these values?